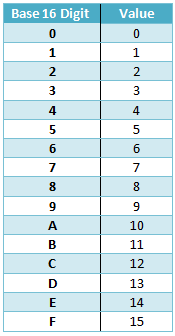
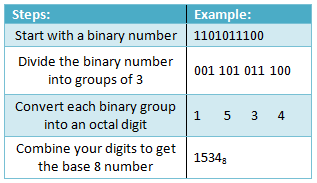
, antal systemer: en introduktion til binære, hexadecimal, og mere,,,,, 18,,,,,,,,, 18,,,,,,,,,, det cyber - mandag envato tuts + kurser vil blive reduceret til $3.- og' t miss.,, aldrig se skøre binære tal og spekulerer på, hvad de mente?se numre med breve blandet og spekulerer på, hvad der foregår?du vil finde ud af alt dette og mere i denne artikel.hexadecimal behøver ikke være skræmmende.,,, afrika (lodret linje: afrika; skriftstørrelsen: mindre;} sup (vertikale linje: super; skriftstørrelsen: mindre;}, er det først og fremmest definitionen af blot.for at få en værdi af et nummer i blot, vi følger det mønster.her er et par eksempler:,,, 892 = 8 * 10,2, + 9 * 10,1, + 2 * 10,0,,,,. 1147 = 1 * 10,3, + 1 * 10,2, + 4 * 10,1, + 7 * 10,0,,,, 53 = 5 * 10,1, + 3 * 10,,,, jeg indrømmer, at dette virker lidt fjollet.vi ved alle, hvilken værdi, blot fordi vi altid er blot, og det er naturligt for os.vi ses snart, hvis vi forstår mønstre på baggrund af blot, vi kan forstå andre baser bedre.,, base-8, om at base-8, også kaldet oktale.base-8: hvad er lyder: ordningen er baseret på det nummer otte (i modsætning til 10).kan du huske, hvordan i blot vi havde ti cifre?nu, i base-8, vi er kun otte cifre: 0, 1, 2, 3, 4, 5, 6 og 7.der er ikke sådan noget som 8 eller 9. vi tæller på samme måde, som vi normalt ville gøre, undtagen med otte cifre.i stedet for en lang forklaring, blot prøver demo - under ved at klikke "tæller 1" for at se, hvordan regner i base-8 fungerer.du bør bemærke, at et lignende mønster til før og efter vi kommer til 7, vi løber tør for forskellige tal for et højere antal.vi har brug for en måde at repræsentere otte af noget.så tilføjer vi et andet ciffer, ændre 7 til 0, og ende med 10.vores svar på 10 i base-8 nu repræsenterer det, vi normalt ville opfatte som 8 i blot. tale om tal skrevet i flere forskellige baser, kan være forvirrende.for eksempel, som vi netop har set, 10 i base-8 er ikke det samme som på blot 10.så fra nu af, vil jeg bruge standardformatet, hvor et indeks, angiver den base af tal, hvis det er nødvendigt.for eksempel, vores base-8 version af 10 nu ligner 10,8,.,, omstilling fra blot at base-8, omstilling fra blot at base-8 er lidt sværere, men stadig direkte.vi er nødt til at vende processen fra oven.lad os starte med et eksempel: 150,10,.,, vi først finde den største magt af 8. det er mindre end vores nummer.her er 8,2 eller 64 (8,3, 512).vi tælle, hvor mange grupper af 64, kan vi tage fra 150.det er 2, så det første ciffer i vores base-8 nummer 2.vi har nu tegnede sig for 128 ud af 150, så vi har 22 tilbage. den største magt af 8. det er mindre end 22 er 8,1, (dvs. 8).hvor mange grupper af 8 kan vi tage fra 22?to grupper, og dermed vores andet ciffer er 2. endelig er vi tilbage med 6, og naturligvis kan tage 6 grupper fra dette, vores sidste cifre.vi ender med 226,8,.,, der kan gøre denne proces en smule klarere med matematik.her er skridt:,, 150 /8,2 = 2 resterende 22, 22 /8, = 2, del 6, 6 /8,0 = 6, vores endelige svar er så alle vores ikke - sidste cifre, eller 226.bemærker, at vi stadig begynder, divideres med den højeste effekt af 8. det er under vores nummer.,, at behandle ethvert grundlag, er det vigtigt at være i stand til at anvende de principper, vi har lært om base-8 og blot til en base.lige så base-8 havde otte cifre og blot havde ti cifre, en base har samme antal cifre som sit grundlag.så base-5 har fem cifre (0 - 4), base-7 har syv cifre (06) osv. lad os se at finde blot værdien af ethvert nummer i en base.vi arbejder i base-b, hvor b, kan være et positivt tal.vi har en række d 4, d, 3, d - 2, d. 1, d, 0, hvor hver d er et ciffer i et nummer.(indeks, her må ikke henvise til basen af antallet, men blot skelne hvert ciffer). vores blot værdi er simpelthen, d, 4 * b, 4, + d, 3 b, 3, + d, 2 b, 2 + d, 1 b, 1. + d, 0, * b, 0,,., her er et eksempel: vi har antallet 32311 i base-4.bemærk, hvordan vores nummer er kun cifre fra 0 til 3, idet base-4 har kun fire samlede tal.vores blot værdi, 3 * 4,4 + 2 * 4,3, + 3 * 4,2 + 1 * 4,1 + 1 * 4,0, = 3 * 256 + 2 * 64 + 3 * 16 + 1 * 4 + 1 * 1 = 949,.vi kunne naturligvis følger dette mønster med et beløb af cifre i vores nummer.,, base-16, base-16 kaldes også hexadecimal.det er almindeligt anvendt i edb - programmer, så det er meget vigtigt at forstå det.lad os begynde med at tælle i hexadecimal for at sikre, at vi kan gennemføre det, vi har lært om andre baser, så langt. da vi arbejder med base-16, vi har 16 cifre.så vi er 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...og hallo!vi løber tør for fingre, men vi skal stadig bruge seks mere.måske kunne vi bruge noget som en ring omkring 10?sandheden er, - - at vi kunne, men det ville være irriterende for type.i stedet har vi bare brug bogstaver i alfabetet, startende med og fortsat f. her er en tabel med alle cifre i base-16:,, andre end disse ekstra cifre, hexadecimal er ligesom enhver anden base.for eksempel, lad os omdanne 3d, 16, at blot.efter de tidligere regler, vi har:, 3d, 16 = 3 * 16,1, + 13 * 16 = 48 + 13 = 61.så 3d, 16, er lig med 61,10,.bemærk, hvordan vi bruger d er værdien af 13 i vores beregning. vi kan omstille sig fra blot at base-16 svarende til den måde, som vi gjorde med base-8.lad os gøre 696,10, base-16.først finder vi den største magt af 16, der er mindre end 696,10,.det er 16,2, eller 296.så: 696 /16,2 = 2 resterende 184184 /16,1 = 11 resterende 8,8 /16,1 = 8 resterende 0, er vi nødt til at erstatte 11 med sin finger repræsentation b, og vi får 2b8,16,., er du velkommen til at prøve noget mere omregninger til praksis.du kan bruge anvendelse under for at kontrollere, at deres svar:,, binære!(base-2), den berømte base-2, også kaldet binær.når alle ved binære består af 37 og 1s, det er vigtigt at forstå, at det ikke er anderledes end nogen anden base matematisk.der er en gammel vits, der lyder sådan her:,,,, kan du finde ud af, hvad det betyder?lad os prøve et par ændringer med base-2.først skal vi gøre 101100,2, blot.vi har:, 101100 = 1 * 2,5, + 1 * 2, 3 + 1 * 2,2, = 32 + 8 + 4 = 44,10,,., lad os omdanne 65 til binære.2,6 - er den højeste effekt på 2 mindre end 65, så:,, 65 /2,6 - = 1. del 1 /2,5 = 0 resterende 1,1 /2,4, = 0 resterende 1,1 /2, 3 = 0 resterende 1,1 /2,2, = 0 resterende 1,1 /2,1, = 0 resterende 1,1 /2,0 = 1 resterende 0, og derfor får vi vores binære tal, 1000001. forståelse af binære er meget vigtigt.jeg har vedlagt en tabel til at påpege cifre "værdier, f.eks. værdien af 10001 er 17, som er summen af værdierne af de to 1 ciffer (16 + 1).det er ikke anderledes, end vi tidligere har gjort, det er bare præsenteres i en let at læse.,, tricks og tips, normalt ved omregning mellem to baser, der ikke blot, at du ville gøre noget som dette:,, omdanne nummer til blot at omdanne resultat ønskede base, der imidlertid er en trick, som vil lade dig omvende mellem binære og hexadecimale hurtigt.først tage binært tal og deler dets cifre i grupper på fire.så siger vi har antallet 1011101,2,.delt op, vi har 0101 1101.se, hvordan vi kan tilføje ekstra nuller til fronten af den første gruppe at gøre grupper af 4.vi finder den værdi for hver gruppe, som hvis det var sit eget nummer, som giver os 5 og 13.vi bruger simpelthen den tilsvarende hexadecimal cifre til at skrive base-16 nummer, 5d, 16. kan vi gå i den modsatte retning, også ved at omregne hver hexadecimal ciffer i fire binære tal.prøv at b7,16, binær.du burde få 10110111,2,., det virker, fordi 16 er en effekt på 2.det betyder, at vi anvender samme trick for base-8, som også er en strøm af 2:,, selvfølgelig, du kan vende processen om at gå fra base-8 til binære.,, indgåelse, lad os gå hele vejen tilbage og revidere farve gætteleg.,, flash, farver er oplagret som et enkelt nummer.når den omregnes til hexadecimal, de to første cifre repræsenterer mængden af røde, de næste to størrelsen af de grønne, og de to sidste størrelsen af den blå.så hvis vores farve er 17ff18,16 vi nemt kan sige, at vores røde komponent er 17,16, eller 23,10,.vores grønne komponent er ff, 16, eller 255,10,.endelig vores blå komponent er 18,16, eller 24,10,.hvis vi får blot version af vores farve, 1572632,10, er vi nødt til at konvertere det til hexadecimal, før vi kan fortælle noget om det.prøv den spil igen, - - og se, hvor meget mere, du kan gøre., forståelse af forskellige antal systemer, er yderst nyttige på mange edb - relaterede områder.binære og hexadecimale er meget almindelige, og jeg vil opfordre dem til at blive bekendt med dem.tak fordi du læste - jeg håber, du har lært meget af denne artikel.de er fri til at tage kildekode fra nogen af de folk.også, hvis du har nogen spørgsmål, så spørg dem nedenunder.