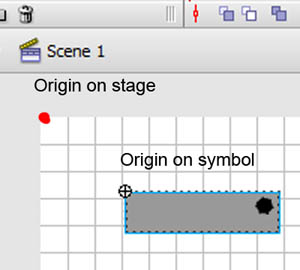
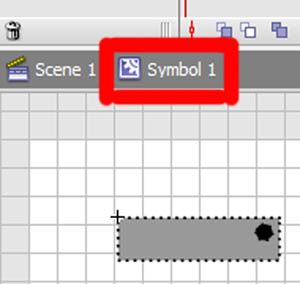
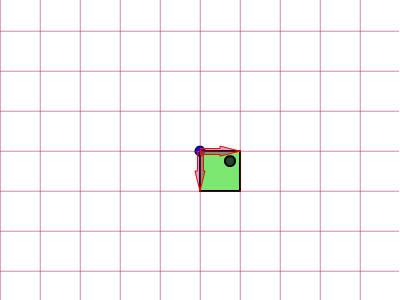
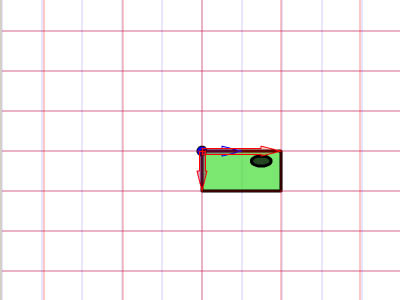
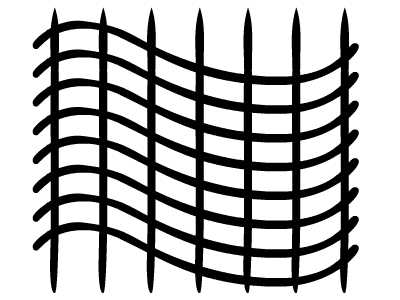
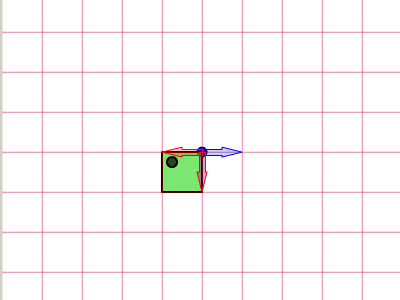
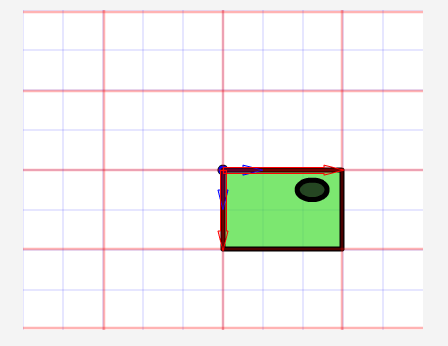
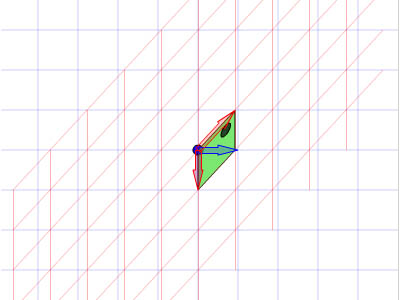
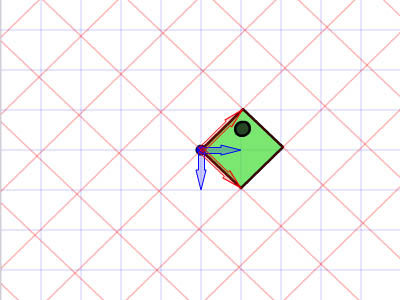
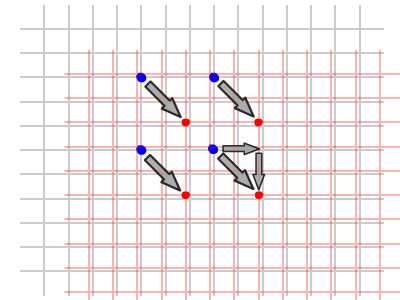
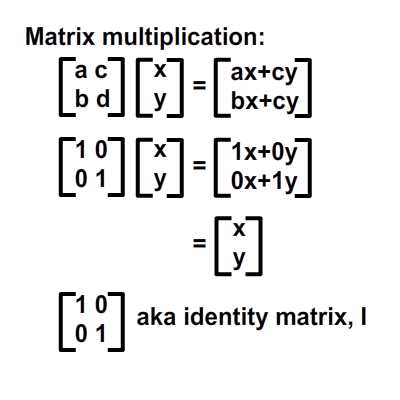
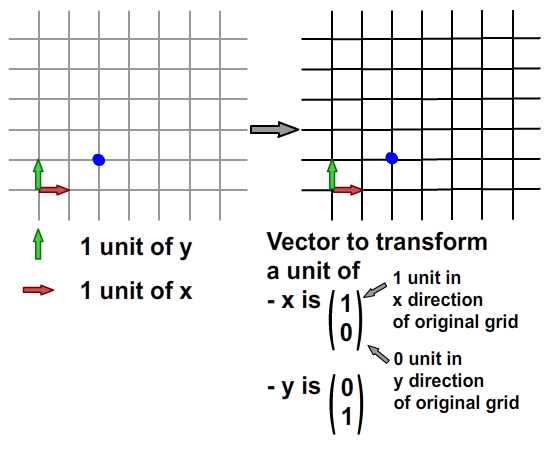
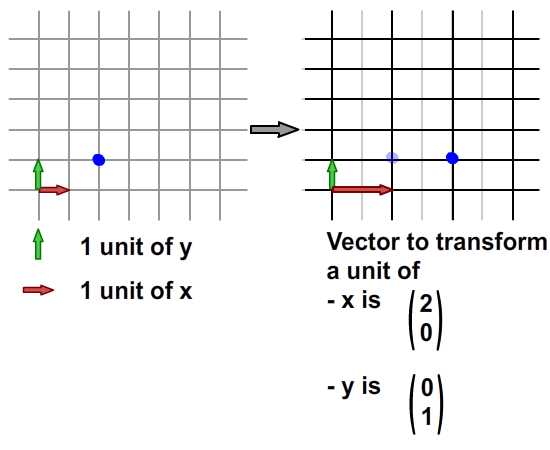
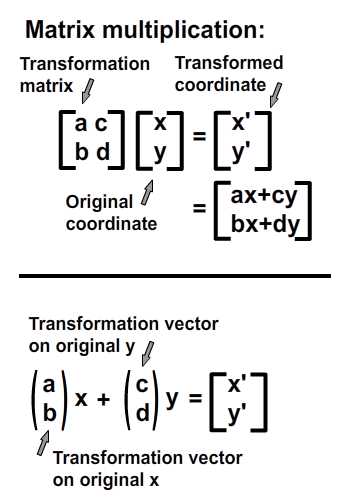
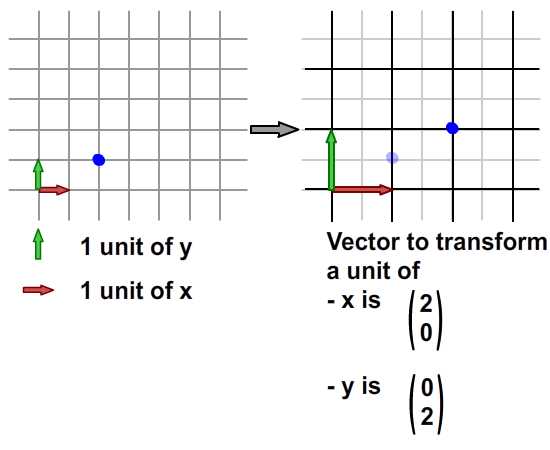
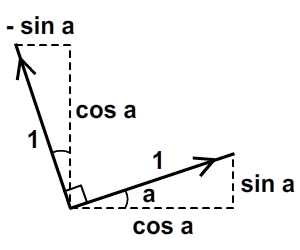
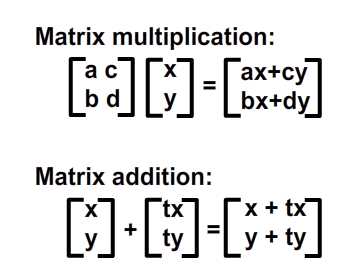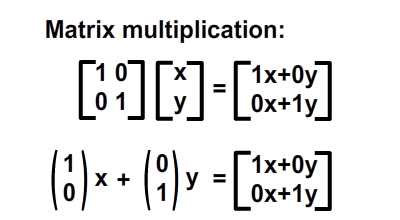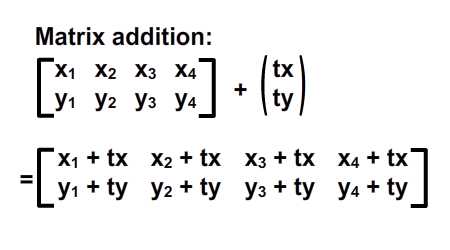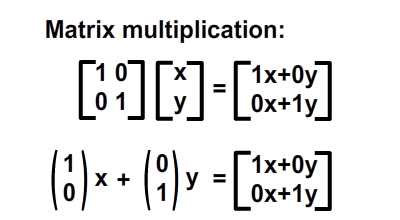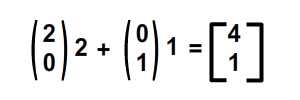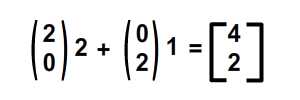, forståelse affine forandringer med matrix matematik,,,,, 15,,,,,,,,, 7,,,,,,, det cyber - mandag envato tuts + kurser vil blive reduceret til $3.- og' t miss. denne post er en del af en serie, ringede du? cirkulær bevægelse i as3: en bevægende kredsløb anotherthe matematik og actionscript af kurver: tegning kvadratiske og tyndkødet kurver, der er inspireret af prof. wildberger i hans forelæsning serie om lineær algebra, agter jeg at gennemføre sit matematiske idéer med flash.vi skal ikke fordybe os i den matematiske manipulation af matricer med lineær algebra. kun via vektorer.denne forståelse, selv om fortynding af elegance af lineær algebra, er nok til at sende os til nogle interessante muligheder for 2x2 matrice manipulation.det, vi især vil bruge det til at anvende forskellige klipning, skævvridning, skifter, og reduktionen af virkninger til billeder på runtime.,,,, endelige resultat forpremiere, lad os tage et kig på det endelige resultat, vi arbejder hen imod.tryk fire retningsbestemte nøgler, op, ned, venstre, højre, - - for at se nogle virkninger, vi kan opnå med affine forandringer.,, hvis du kun bruge venstre og højre pil nøgler, fisk, ser ud til at svømme rundt i en pseudo-3d isometriske rummet.,, trin 1: forskellige koordinere rum, grafik er trukket på koordinere rum.så for at manipulere med dem, navnlig for at oversætte, drej, omfanget, afspejler og hældning grafik, er det afgørende, at vi forstår at koordinere rum.vi generelt gøre brug af ikke blot én, men flere koordinere rum i et enkelt projekt - og det gælder ikke kun for designere ved hjælp af flash - ide, men også for programmører skriftligt actionscript. i flash ide det sker når du veksle din tegninger i movieclip symboler: hvert symbol har sin egen oprindelse, er, at billedet ovenfor. viser oprindelsen af scenen, koordinere rum (rød prik), og at de symbol er koordinere rum (registrering punkt præget af crosshair).at vide, hvilken plads, du er i øjeblikket, at overholde bar under tidslinjen for flash - ide, som det fremgår af billedet nedenfor.,, jeg bruger flash cs3, så dens placering, kan være forskellige for cs4 og cs5). det, jeg gerne vil understrege, er eksistensen af forskellige koordinere rum, og det faktum, at du allerede er vant til at bruge dem.,, trin 2: den logiske begrundelse, er der en god grund til det.vi kan bruge en koordinering af rummet som en reference for at ændre andre koordinere rum.det lyder måske fremmed, så jeg har medtaget flash præsentation nedenfor for at lette min forklaring.klik og slæbe den røde pile.lege med det. i baggrunden er en blå net, og i forgrunden er en rød - nettet.den blå og røde pile i x - og y - akse i overensstemmelse med de for flash - koordinere rum, hvis center har jeg flyttet til midt på scenen.den blå koordinat er referencesystemet, gridlines vil ikke ændre sig, som du kan interagere med den røde pile.den røde felt, på den anden side kan omlægges, og især ved at trække den røde pile, konstaterer, at den pil angiver også en vigtig ejendom af disse net.de angiver, om en enhed af x, og en enhed af y på deres respektive net.der er to røde bånd på den røde felt.hver af dem angive længden af en enhed på x - aksen og y - aksen.de dikterer, orientering af koordinere rum.lad os tage den røde pil peger på x - aksen og udvide det til at være dobbelt så lang tid som den oprindelige pil (vist i blå).overholde følgende billeder, ser vi, at billedet (den grønne boks), trukket på den røde net er nu strakt vandret, på grund af den kendsgerning, at den røde net er det, der er på nu er dobbelt så store.det, jeg prøver at sige, er ret enkel: du kan bruge en koordinering af rummet som et grundlag for at ændre et andet koordinere rummet.,, trin 3: affine koordinere rum, så hvad er en "affine koordinere rum"?jeg er sikker på, at du er forsigtig nok til at konstatere, at disse koordinere rum på grundlag af parallelle net.lad os tage den røde affine rum for eksempel: der er ingen garanti for, at både den x - aksen og y - akse er vinkelret på hinanden, men de kan være forvisset om, at vi forsøger at pirre pile, vil du aldrig nå frem til en sådan sag som nedenfor.,,, det koordinerer rummet er ikke en affine koordinere rummet.faktisk, x - og y-axes sædvanligvis henviser til de kartesiansk koordinere rum, som vist nedenfor.,, konstaterer, at den horisontale og vertikale net er vinkelret på hinanden.kartesiske er en type, affine koordinere rummet, men vi kan ændre det til andre affine rum, som vi foretrækker.den horisontale og vertikale net, ikke nødvendigvis skal være vinkelret på hinanden.,,, eksempel på en affine koordinere rum, et eksempel på en affine koordinere rum, trin 4: affine forandringer, som du måske har gættet, affine transformationer oversættelse, afskalning, refleksion, skævvridning og rotation,.,,, oprindelige affine rum, især affine rum, der afspejles affine rum, er affine rummet, skift og skaleres affine rummet, det siger sig selv, at fysiske egenskaber såsom, x, y, scalex, scaley og rotation, afhænger af rummet.når vi kræver, at disse egenskaber, er vi faktisk, at affine koordinater.,, løntrin 5: forståelse af matrix, håber jeg, de billeder, ovenfor, er tydelige nok til at køre hjem, det er en god idé.det er, fordi en programmør arbejder med flashdevelop, vil vi ikke se de net, der flash "belejligt displays til designere.alle disse er nødt til at leve i dit hoved, bortset fra at disse net, er vi også nødt til at ty til matrix, klasse.efter således at have en matematisk forståelse af matricer, er vigtigt, så vi skal revidere driften af matrix: supplement og formering, trin 6: geometriske betydningen af matrix over matrix operationer convery betydninger geometrisk.med andre ord, du kan forestille dig, hvad de mener om en figur.lad os antage, at vi har fire punkter i vores koordinere rum og ønsker at flytte dem til et sæt nye steder.dette kan gøres ved hjælp af matrix over.se billedet nedenfor. som du kan se, er vi rent faktisk at omlægge hele den lokale koordinere rum (røde net), hvor disse fire punkter er trukket.betegnelsen for udførelsen af disse aktiviteter er som vist nedenfor, kan vi også se, at denne ændring faktisk kan være repræsenteret ved hjælp af en vektor for (tx, ty).lad os skelne vektorer og statisk punkter i koordinere områder af vores brug af parenteser og firkantede parenteser.jeg har skrevet om dem på billedet nedenfor.,, trin 7: actionscript gennemførelse, her er en simpel gennemførelse af matrix over.se bemærkninger: offentlige klasse over udvider sprite {offentlige funktion addition() {var m: matrix = nye matrix(); //instantiate matrix m.tx = stage.stagewidth * 0, 5; //forskydning i x m.ty = stage.stageheight * 0, 5; //skift i y var d: dottedbox = nye dottedbox(); //skabe skik grafisk (stiplet boks er en sprite) addchild (d) d.transform.matrix = m //anvender matrix til vores grafisk}}, trin 8: geometriske betydning af matrix formering, matrix formering er noget mere avanceret end matrix over men prof. wildberger er elegant brudt det ned til denne enkle fortolkning.jeg vil ydmygt forsøg på at gentage hans forklaring.for dem, der ønsker at dykke dybere ned i forståelsen af lineær algebra, der fører til det, se professorens forelæsningsrækker. lad os starte ved håndteringen af tilfælde af identitet matrix, i., fra billedet ovenfor, ved vi, at multiplicere en vilkårlig matrix, en af identiteten matrix, -, vil altid medføre a. her er en analogi: 6 x 1 = 6; identitet matrix er sammenlignet med nummer 1 i denne multiplikation. alternativt kan vi skrive den resulterer i følgende vektor - format, som i høj grad vil forenkle vores fortolkning:, den geometriske fortolkning af denne formel er vist i billedet nedenfor.,, fra de kartesiansk net (venstre skala), kan vi se det blå punkt ligger på 2, 1).hvis vi var at ændre det oprindelige net af x - og y - til et nyt net (net) i henhold til en fastsat af vektorer (under ikke - nettet), det blå punkt vil blive flyttet til (2, 1) om de nye net - men når vi kort den tilbage til det oprindelige net, det er det samme som før.fordi vi omdanner det oprindelige net til et andet gitter, der deler de samme vektorer for x - og y - vi kan ikke se forskel.faktisk er de ændringer af x - og y - i denne ændring er lig nul.det er, hvad det betød for identitet matrix, fra en geometrisk synspunkt. men hvis vi forsøger at foretage en kortlægning af andre ændringer, vil vi se en forskel.jeg ved, det var ikke det mest oplysende eksempel til at begynde med, så lad os gå videre til et andet eksempel.,, trin 9: mere langs x, image ovenfor viser en nedskæring af koordinere rum.tjek vektor for x i omdannet koordinere rummet: en enhed af omdannet x står for to enheder af den oprindelige x. om ændret koordinere rummet, koordinering af det blå punkt er stadig (2, 1).men hvis du prøver at kortlægge dette koordinere fra omdannet net på det oprindelige net er det (, 4, 1). denne idé er fanget af billedet ovenfor.hvad med formlen?resultatet skal være sammenhængende, lad os tjekke det ud. jeg er sikker på, at du husker disse formler.jeg har tilføjet deres respektive betydninger.,,, for at tjekke ud af det numeriske resultat af vores mål, f.eks.,, oprindelige koordinere (2, 1), vektor for omdannet x - akse: (2, 0), vektor for omdannet y - akse: (0, 1), forventede resultat: (2 * 2 + 0 * 1, 0 * 2 + 1 * 1) = (4, 1), de er enige med hinanden.nu kan vi heldigvis gælder denne idé til andre forandringer.men før det, en actionscript gennemførelse.,, trin 10: actionscript gennemførelse, tjek actionscript gennemførelse (og den deraf følgende stg) nedenfor.bemærker, at en af overlappende felter strækkes langs x af en skala fra 2.jeg har fremhævet vigtige værdier.disse værdier vil blive justeret i de senere trin til at repræsentere forskellige forandringer. offentlige klasse formering udvider sprite {offentlige funktion multiplication() (var - ref: dottedbox = nye dottedbox(); //skabe reference grafisk addchild (dommer); ref.x = stage.stagewidth * 0, 5; ref.y = stage.stageheight * 0, 5; var m: matrix = nye matrix(). //instantiate matrix m.tx = stage.stagewidth * 0, 5; //forskydning i x m.ty = stage.stageheight * 0, 5; //skift i y m.a = 2, m.c = 0, m.b = 0, m.d = 1; var d: dottedbox = nye dottedbox(); //skabe skik grafisk addchild (d) d.transform.matrix = m //anvender matrix på vores grafisk}}, trin 11: reduktionen af x - og y -, her har vi besteg nettet af fact, eller af to langs x - og y-axes.det blå punkt er på 2, 1) i det oprindelige net før omdannelsen og 4, 2) i det oprindelige net efter transformation.- selvfølgelig er det stadig på 2, 1) i den nye, nettet efter omdannelsen.), og til at bekræfte resultatet numerisk...,,,,,,,de matcher igen!se det i actionscript gennemførelse, bare at ændre værdien af, m.d, fra 1 til 2.,, jeg er sikker på, i vil gerne prøve det selv, så gå videre og et, orientering af omdannet y - akse, samtidig med at den x - aksen, orientering af begge akser i alt, - har omfattet flash - output i begge tilfælde, jf. nedenfor.for læsere, der ville have hjælp med disse værdier, se, multiplication_final.as i kilden download.,, trin 14: rotation, mener jeg, rotation en delmængde af gøre.den eneste forskel er, at i vekseldrift, størrelsen af en enhed af x - og y - aksen, både opretholdes, således som det er perpendicularity mellem de to økser.,, actionscript faktisk giver en metode i den matrix, klasse, rotate(), til at gøre dette.men lad os gå det igennem alligevel. vi ønsker ikke at ændre betydningen af en længdeenhed i x - og y - fra det oprindelige net; for at ændre retningslinjerne for hver.vi kan bruge trigonometri for at nå frem til det resultat, som vist i billedet ovenfor.i en vinkel på roation, en, vi får det ønskede resultat ved hjælp af vektorer (cos en synd, for x - aksen og - synd, fordi a) for x - akse.størrelsen af hver ny akse vil stadig være en enhed, men hver akse skal være i en vinkel på et i forhold til den originale. for actionscript gennemførelse, forudsat at den vinkel, der er 45 grader (dvs. 0 * pi radianer), bare nappe matrix - værdier, var følgende: a: antal = 0, 25 * math.pi m.a = matematik. - (en); m.c = - 1 * matematik. synd, litra a), m.b = matematik. synd, litra a), m.d = matematik. - (en); den fulde energikilde kan være, der er omhandlet i multiplication_final.,,, skridt. 15: anvendelse, under en vektor fortolkning af en 2x2 matrice giver plads for os at udforske.dens anvendelse i at manipulere bitmaps (, bitmapdata, linebitmapstyle, linegradientstyle, osv.) er udbredt, men jeg tror, jeg vil gemme det til en anden lektion.i forbindelse med denne artikel, vil vi forsøge at føre vores sprite på driftstid, så det ser ud, som om det er faktisk med i 3d,.,,, på en pseudo-3d isometriske verden, fra billedet ovenfor, kan vi se, at i en verden med isometrisk afbildning, en grafisk, der er "stående" holder sin y - aksen, vektor uændret, mens den x - aksen vektor er roterer.bemærker, at en længdeenhed for x - og y - akse ændrer ikke - med andre ord, at der ikke mere skal ske enten i akse, rotation omkring x - aksen. her er et eksempel på denne idé i flash.klik på scenen og begynde at trække rundt for at se fiskene skævhed.overgang til at stoppe deres samspil.,, her er den vigtige del af actionscript.jeg har understreget den afgørende linjer, der håndterer x - akse rotation.du kan også henvise til, fakeiso.,., private var f1: fisk, m. matrix, private var spredning: punkt; private var axisx: punkt, axisy: punkt; offentlig funktion fakeiso() (spredning = ny litra stage.stagewidth * 0, 5, stage.stageheight * 0, 5); m = nye matrix(); m.tx = spredning. x; m.ty = spredning. y. //flytte til midten af trin (= nye fish(); addchild (f1); f1.transform.matrix = m //anvendelse omdannelse til på fisk axisx = det nye punkt (1, 0); //vektor for x - akse axisy = det nye punkt (0, 1); //vektor for y - akse. addeventlistener (mouseevent.mouse_down, start); //start interaktion fase. addeventlistener (mouseevent.mouse_up, slut); //ende interaktion} privat funktion start (e: mouseevent): ugyldig (f1. addeventlistener (event.enter_frame, ajourføre)} privat funktion (e: mouseevent): ugyldig (f1. removeeventlistener (event.enter_frame, ajourføre)} privat funktion ajourføring (e: begivenhed): ugyldig (axisx. derfor (mousex - f1. x, mousey - f1. y); //bestemme orientering (men størrelsen ændret - axisx. normalisere (1) //fastsætte omfanget af vektor med nye orientering til 1 enhed apply2matrix(); //anvender matrix på fisk) privat funktion apply2matrix (): ugyldig (m.setto (axisx. x, axisx. y, axisy. x, axisy. y, spredning. x, spredning. y); f1.transform.matrix = m}, her har jeg brugt punkt klasse til opbevaring af vektorer, trin 16: tilføje tastatur kontrol i dette skridt, vil vi forsøge at tilføje tastatur kontrol.fisken er placering vil opdatere i henhold til den hastighed, velo,.vi skal definere trin for positive (uret) rotation og negative (mod uret) rotation samt., velo = det nye punkt (1, 0); //velo vil blive brugt til at definere x - aksen axisy = det nye punkt (0, 1); delta_positive = nye matrix(); delta_positive. drej (math.pi * 0,01); //positiv drejning delta_negative = nye matrix(); delta_negative. drej (math.pi * - 0, 01); //negativ drejning på centrale presse velo, roterer:, privat funktion keyup e: keyboardevent): ugyldig (hvis (e.keycode = = tastatur. venstre) {velo = delta_negative. transformpoint (velo) //roterer velo urets} andre, hvis (e.keycode = = tastatur.) {velo = delta_positive. transformpoint (velo) //roterer velo uret), for hvert billede, vi skal forsøge at farveforsiden af den fisk, og vrider den fisk.hvis den hastighed, velo, har et omfang på mere end 1 og anvendes til fisk er matrix, m, vil vi få en mere kraft - - for at fjerne denne mulighed, vi skal normalisere hastighed og kun anvendes til fisk, privat funktion ajourføre matrix. e: begivenhed): ugyldig (var - front_side: boolean = velo. x > 0 //kontrol på forsiden af fisk, hvis (front_side) (f1. colorbody (0x002233,0.5) //farve forsiden af fisk, andre f1. colorbody (0xffffff, 0, 5) //hvid anvendes til tilbage side af fisk spredning = spredning. der tilsættes (velo); //ajourfører løbende forskydning med hastighed var velo_norm: punkt = velo. clone(); //i sag velo > 0, vi har brug for at foretage en ny beregning af 1 enhed, af længde for x. velo_norm. normalisere (1) //note, som x - aksen mere end 1 vil udføre mere.vi vil ikke have, at nu m.setto (velo_norm. x, velo_norm. y, axisy. x, axisy. y, spredning. x, spredning. y); f1.transform.matrix = m}, skridt 17: dine fisk, klik på scenen, så tryk i venstre og højre pil nøgler til at se den fisk, ændring retning.,, gå 18: et tastatur kontrol, at krydre tingene op, lad os tillade kontrol med y - aksen, vektor -., privat funktion keyup e: keyboardevent): ugyldig (hvis (e.keycode = = tastatur. venstre) {velo = delta_negative. transformpoint (velo)} andre, hvis (e.keycode = = tastatur.) {velo = delta_positive. transformpoint (velo)} hvis (e.keycode = = tastatur.) (axisy = delta_negative. transformpoint (axisy)} andre, hvis (e.keycode = = tastatur.) (axisy = delta_positive. transformpoint (aksey)), at fastlægge forsiden af fisk, er vi nu nødt til at indarbejde y - aksen.her er koden til:, var front_side: boolean = velo. x * axisy. y > 0, hvis (front_side) (f1. colorbody (0x002233,0.5)} andre f1. colorbody (0xffffff, 0, 5), trin 19: din ikke så almindelige fisk, men for nogle resultatet af kontrollen begge akser, kan vise sig at være en smule forvirrende, men pointen er, at du nu kan føre deres fisk, oversætte, afspejler det, og drej den!prøv det band på + venstre. højre, ned + venstre, +.,,, se om du kan opretholde "foran" side af fisk (fisk, vil blive grayed).tip: tap op hele tiden, så til venstre, og så ned, og så til højre.du er en rotation!indgåelse, håber jeg, du finder matrix matematik værdifuld for deres projekter, efter at have læst den artikel.jeg håber, at skrive lidt mere om ansøgninger med 2x2 matrix i små hurtige tips sig ud af denne artikel og om, matrix3d, som er afgørende for 3d manipulationer.tak for at læse, - tak.