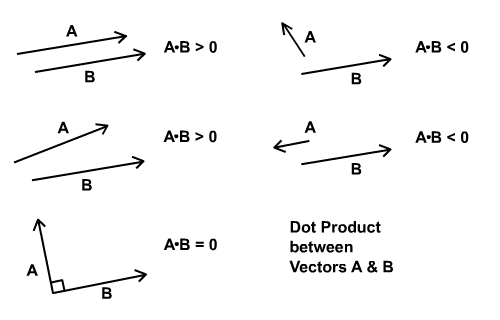
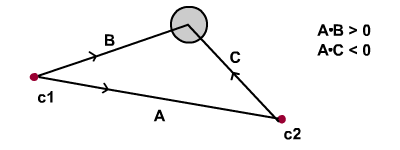
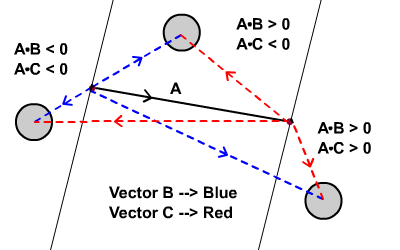
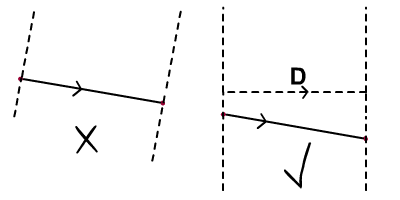
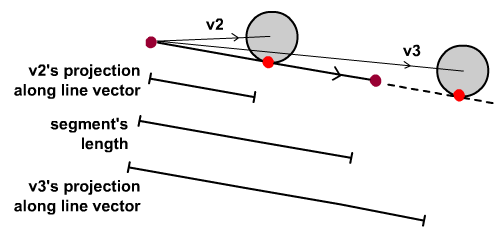
, hurtigt tip: kollision detektering mellem en cirkel og et linjesegment,,,,, 2,,,,,,,,, 10,,,,,,, det cyber - mandag envato tuts + kurser vil blive reduceret til $3.- og' t miss. denne post er en del af en serie kaldet kollision påvisning og reaktion. hurtig tip: kollision detektering mellem en cirkel og en linequick tip: kollision reaktion mellem en cirkel og et linjesegment, vi dækkede kollision detektering mellem en uendelig linje og cirkel i vores tidligere hurtigt drikkepenge.men de spørgsmål, der opstod, var, at den strækker sig længere end den synlige linjesegment. den strækker sig til en hyperplane.i denne hurtige tips, vil vi begrænse vores sammenstød påvisning til en linje, segment,.,,,, endelige resultat inden, vi skal arbejde hen imod dette resultat:,, klik begynder knap til at flytte de kredse i toppen af scenen.,, trin 1: to fremgangsmåder, der er talrige metoder til at begrænse kollision påvisning i et linjesegment.skal vi se på to metoder, denne gang.den første fremgangsmåde er lidt mere strengt matematisk end den anden, men det er to begreber, som, hvis du forstår godt, utvivlsomt vil være til gavn for dem i fremtiden.begge fremgangsmåder manipulere dot produkt er karakteristisk for at være en målestok for, hvor parallelle to givet vektorer. lad os se på det første.hvis a og b er vektorer.hvis a og b er parallel - eller i det mindste peger i samme retning - dot vare mellem a og b, vil give et positivt tal.hvis a og b er rettet modsat hinanden - eller i det mindste peger i modstridende retninger - dot vare mellem a og b, vil give et negativt tal.hvis a og b er ortogonale (udgør 90 ° til hinanden, så de dot produkt vil føre til 0.nedenstående diagram viser denne beskrivelse,.,, trin 2: vedrører dot - produkt til betingelser, vil vi nødt til at danne vektorer b og c fra begge ender af linjesegment, således at deres dot produkt med linjesegment er vektor, kan afgøre, om cirklen er i segmentet, overholde diagrammet nedenfor..hvis den cirkel, inden for segmentet, så værdien af dot vare mellem a og b er positive, og at mellem a og c er negativ,.,, diagrammet nedenfor viser, hvordan dot produkt skifter afhængigt af, om cirklen er over eller strækningssegmentet.note forskellene i værdien af dot produkt.,, bemærker også, at "strækningssegmentet" betyder ikke nødvendigvis, at den cirkel, skærer linjesegment, at det falder inden for de to tynde linjer på diagrammet ovenfor. så når kollisionen forekommer mellem linje og cirkel, som vi har set det i den tidligere hurtigt tip, er vi nødt til at undersøge, om den cirkel er placeret strækningssegmentet.hvis det er, så ved vi med sikkerhed, at der er en reel vejkryds.,, trin 3: gennemførelse, trin 2, forklarede begrebet, vi bruger til at begrænse kollision påvisning er strækningssegmentet.der er dog stadig en mangel på præcision.ser du, det område, der er defineret, er en lille vippes; vi bør sigte mod at bruge det område, der er defineret i nedenstående diagram.,, det er let. vi ganske enkelt beregne d som en horisontal projektion af a. så i stedet for at bruge en, vi bruger d til dot produkt med b og c. alle de betingelser, som forklaret i trin 2 står stadig, men i stedet for skrå segment, vi har defineret en vertikal område. denne korrektion kan være visuelt værdsat hvis cirklen er stort. hvis cirkel var små, dets center ville være så tæt på den holdning, at det visuelle fejl ville være svært at opdage, så vi kunne komme væk med det let skråt område og spare nogle datafortroligheden. alligevel vil jeg forsøge at gøre tingene på den rigtige måde.du kan hente din tilgang ved at ændre betingelsen lidt.,, trin 4: gennemførelse, den første actionscript snippet her opstiller vektor d (, v_line_onx) //att2: den vandrette vektor var line_onx: antal = linje. projectionon (nye vector2d (1, 0)); v_line_onx = nye vector2d (1, 0); v_line_onx. setmagnitude (line_onx);,, note:, vi bruger timer fra min tidligere tutorials her.vector2d blev indført i alvoren i aktion, men du behøver ikke at læse, at bruge den klasse, der er indeholdt i kilden download. den anden actionscript snippet her opstiller b (, c1_circle,) og c (, c2_circle,) og kontrol af sammenstød, og om cirklen er indenfor segmentet eller ikke, privat funktion genopfriske e: begivenhed): ugyldig (for (var - jeg: int = 0. jeg < circles.length; jeg + +) (//beregning af linje vinkelret afstand til bolden var c1_circle: vector2d = nye vector2d (kredse [i]. x - x1, cirkler [i]. - y1) var c1_circle_onnormal: antal = c1_circle. projectionon (leftnormal); //att2: få vektor fra c2 til cirkel var c2_circle: vector2d = nye vector2d (kredse [i]. x - x2, cirkler [i]. y - y2); cirkler [i]. y + =2. hvis (c1_circle_onnormal < = kredse [i]. radius & & v_line_onx. dotproduct (c1_circle) > 0 & & v_line_onx. dotproduct (c2_circle) < 0) (//hvis kollisionen skete, lav bevægelighed kredse [i]. y - = 2}}}, løntrin 5: resultatet, her er resultatet af den første metode.tryk på knappen til at nulstille holdninger i alle kredse til toppen af trin, trin 6: anden tilgang, den anden fremgangsmåde er meget enklere.jeg vil prøve at arbejde baglæns fra den ende denne gang., overholde diagrammet nedenfor.et linjesegment fra c1 til c2.det er klart, at collide1, og collide3, er både uden for linjesegment, og det eneste, collide2 er strækningssegmentet, lad v1, v2 og v3 være vektorer fra c1 til forskellige kredse.kun v2 og v3 er parallel - eller i det mindste peger i samme retning til linjen vektor (c1 til c2).ved kontrol af en positiv værdi i dot vare mellem linjen vektor, og hver af disse vektorer fra c1 til den tilsvarende cirkel centre (v1, v2 og v3) kan man fastslå, at collide1 er ud over linjen segment.med andre ord, c1.v1.,,, det næste, vi skal finde en metode til at fastslå, at collide3 er uden for linjesegment.det burde være let.det er indlysende, at v3 (linjen vektor vil overstige varigheden af linjesegment.vi skal bruge denne egenskab til at luge ud collide3., så lad mig sammenfatte den anden metode:, først tjekker vi for et skæringspunkt mellem den uendelige linje og cirkel. hvis der er et kryds, yderligere at undersøge følgende for at fastslå, om det sker strækningssegmentet:, kontrollere, at en positiv værdi er fremstillet når vi tager dot produkt af vektoren fra c1 til cirkel og den vektor, og kontrollere, at omfanget af projektionen af vektoren linjen vektor er kortere end linjesegment længde.,,, trin 7: gennemførelse, her er actionscript gennemførelsen af ovenstående:, privat funktion - e: begivenhed): ugyldig (for (var - jeg: int = 0. jeg < circles.length; jeg + +) (//beregning af overensstemmelse ervinkelret afstand til bolden var c1_circle: vector2d = nye vector2d (kredse [i]. x - x1, cirkler [i]. y - y1) var c1_circle_onnormal: antal = c1_circle. projectionon (leftnormal); //att2: den relevante vektorer var c1_circle_online: antal = c1_circle. projectionon (line); cirkler [i]. y + = 2; hvis (matematik. abs (c1_circle_onnormal) < = kredse [i]. radius & & linje. dotproduct (c1_circle) > 0 & & c1_circle_online < linje. getmagnitude()) (//hvis kollisionen skete, lav bevægelighed kredse [i]. y - = 2}}}, trin 8: resultatet, i det væsentlige, det vil føre til det samme resultat som den foregående, men da der er et par linjer kode kortere i den anden metode, tror jeg det bedre, c.onclusion håber, det har hjulpet.tak fordi du læste.næste gang, vil vi se på kollision reaktion.