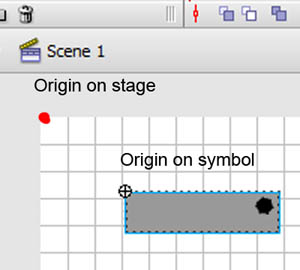
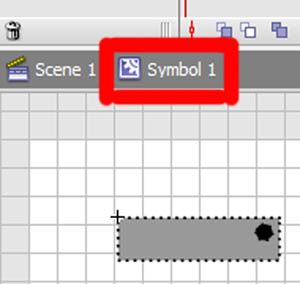
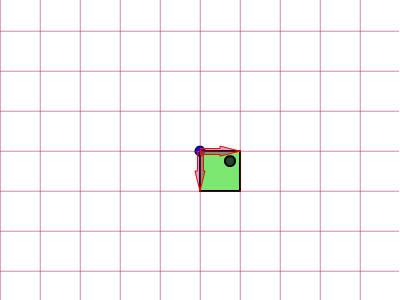
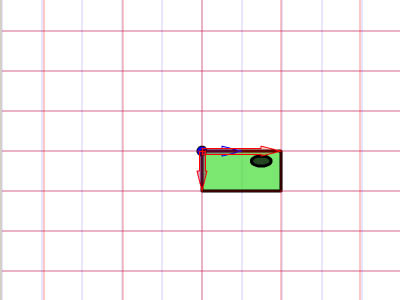
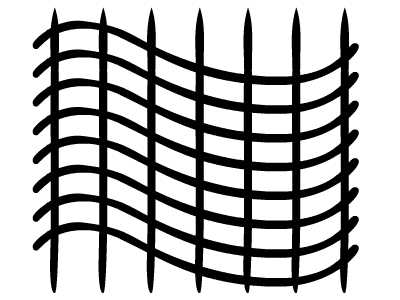
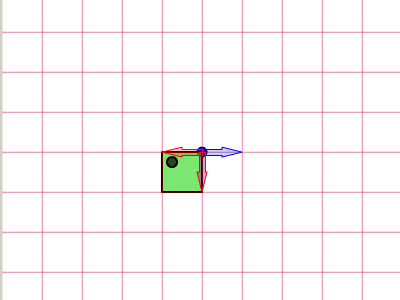
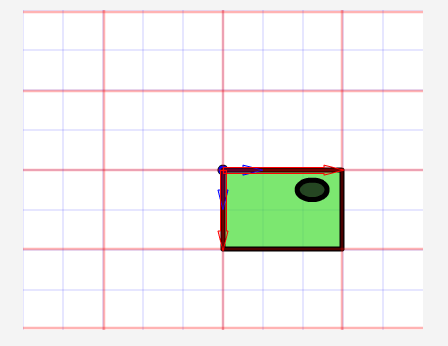
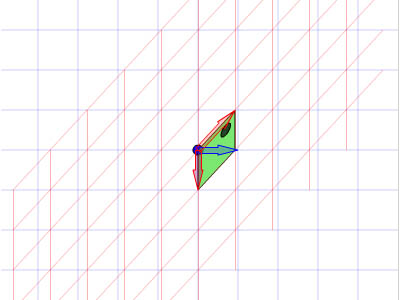
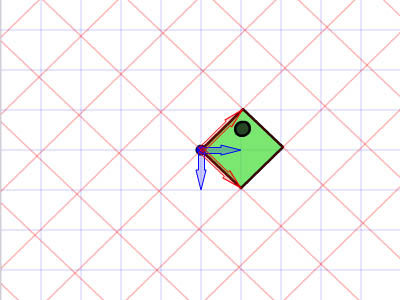
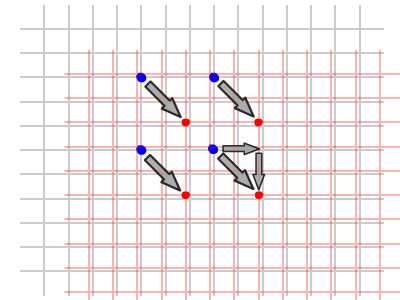
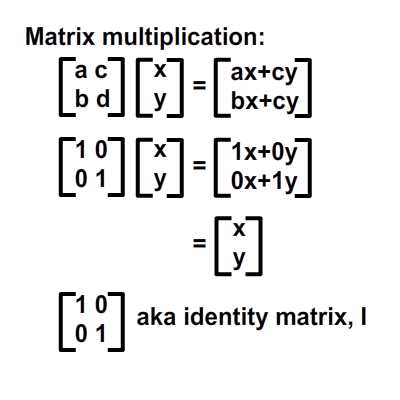
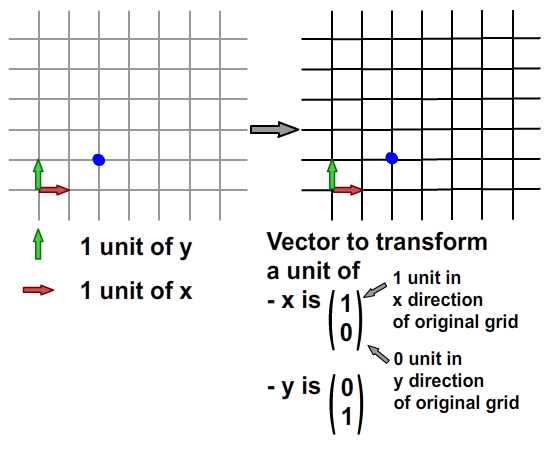
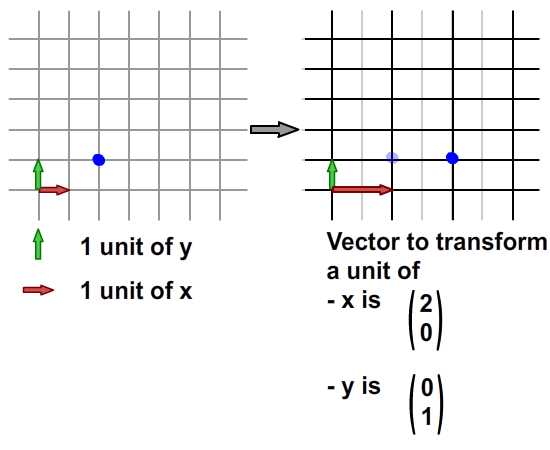
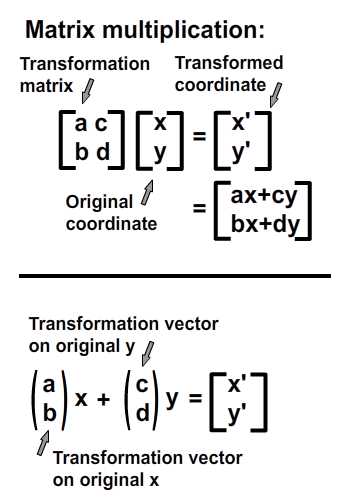
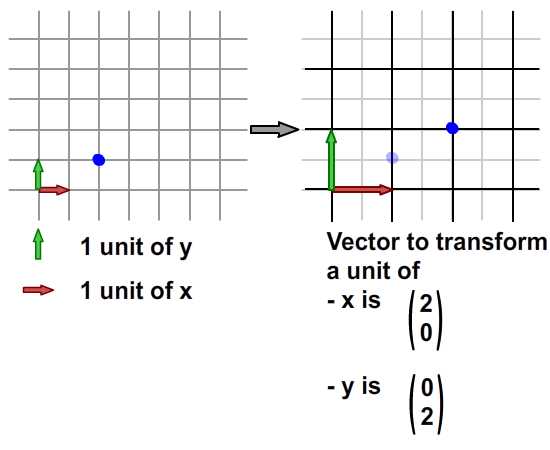
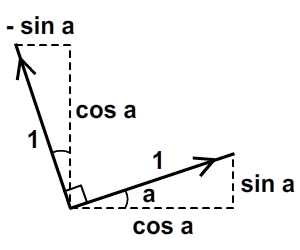
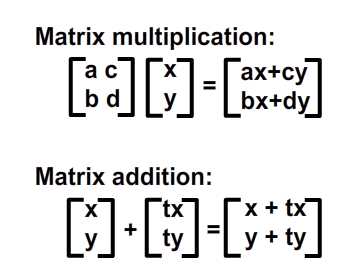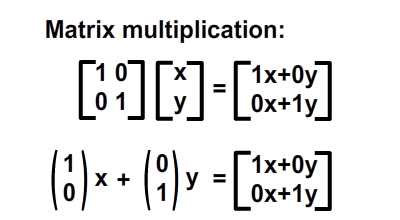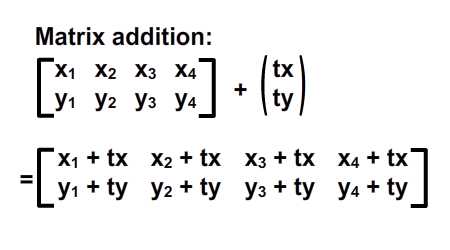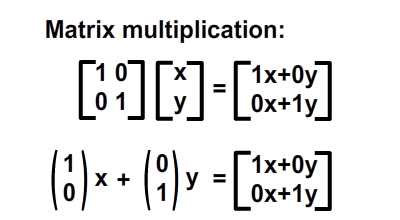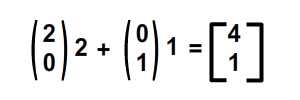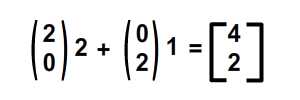begrip affine matrix, wiskunde,,,,,,,,,, 15, 7 - eenheid,,,,,,,, de delen van het netwerk, maandag wat in tuts + koers zal dalen tot slechts drie dollar.Niet' niet missen, een deel van de prijs van een reeks noem je wiskunde doen. In de ontwerpresolutie om 3: een bewegend object van sporen van een wiskundige en behandelingen curve: kaart van de tweede en de derde bocht, geïnspireerd door de 维尔德贝格尔 professor in z 'n lezingen voor Linear algebra, ben ik van plan om met z' n wiskunde. Dacht.We moeten niet door de matrix voor Linear algebra om verder onderzoek te doen naar de wiskunde, maar door de vector.Deze erkenning, hoewel de verdunning van de elegante Linear algebra, is voldoende om ons in een 2x2 matrix die interessante mogelijkheden.In het bijzonder, gebruiken we dat om de toepassing van verschillende teelten, draai, draai, als "beelden,,,, het uiteindelijke resultaat bekijken, laten we eens kijken naar de resultaten van de laatste, we zullen proberen.In de vier belangrijkste richting, onder, links, zien wat kan worden bereikt door gebruik te maken van onze rechten, affine. Als je links en rechts de pijl, vis lijkt te zwemmen in een driedimensionale ruimte, neutraliteit, stap 1: verschillende ruimte, grafische weergave in de ruimte.Dus om te manipuleren, en met name op de rotatie en schaal, reflectie en helling van de grafische, we begrijpen het coördineren van de ruimte is van cruciaal belang.We gebruiken meestal niet slechts één, maar in een enkel project meer coördinatie van het gebruik van de ruimte is niet alleen voor de ontwerpers van Flash ide, ook in het script schrijven. - dat gebeurt, als je de tekeningen in de film... Symbool: elk symbool heeft zijn eigen de oorsprong van deze beeld.,, dat De fase van de coördinaten van de oorsprong van de ruimte (rood), en de coördinatie van de symbolen van de ruimte (van toepassing op de lijn).Weet je de ruimte in de huidige, aan de BAR van de tijdschema 's onder de flash ide zoals hieronder.,, (ik flash CS - 4 en 3, zoals de positie van de verschillende systemen, het kan) wil ik benadrukken dat de coördinatie van de verschillende ruimte bestaat, en dat is u bekend, het feit dat het gebruik van ze. Stap 2: de theoretische basis, en nu is er een goede reden voor.We kunnen gebruik maken van een coördinatie van de ruimte als referentie voor het veranderen van een andere ruimte.Dit klinkt misschien vreemd, dus ik heb omvat de volgende presentaties, zodat mijn interpretatie.Klik op en trek de rode pijl.Op de achtergrond te spelen in een blauwe net bij de receptie is net een rode.De blauwe en rode pijl gaan langs de X - en Y - as in het centrum van de flash - coördinatie van de ruimte, ik ben overgeplaatst naar het midden van het podium.Blauw is een referentie - net; de lijn niet omdat je de rode pijl interactie waargenomen.Rood -, aan de andere kant, kan worden aangepast, door die rode pijl deel ervan op de pijl blijkt dat een van de belangrijkste kenmerken van deze netwerken.Ze zei dat het een eenheid en een eenheid van een eenheid, van hun netwerk.Red rooster heeft twee rode pijl.Die zijn weergegeven in de X - en Y - as van een eenheid van lengte.Zij bepaalt ook de coördinaten van de richting van de ruimte.Laten we een rode pijl op de X - as en de uitbreiding van het twee keer zo lang de pijl (blauw).Nemen het volgende beeld, zien we in het rood, net op die beelden (groene doos) is nu de tekening, als gevolg van de Rode - worden opgesteld tot nu twee keer zo hoog is als in de breedte.Ik probeer te doen, is heel eenvoudig: je kunt gebruik maken van een coördinatie van de ruimte om te veranderen van een andere ruimte, in stap 3: affine ruimte, dus wat is "affine ruimte"?Nou, ik denk dat je moet kijken naar deze coördinaten ruimte met parallelle rooster is geschilderd.Laten we een voorbeeld nemen, rode affine ruimte: er is geen garantie dat de X - en Y - as die loodrecht op elkaar, maar wees gerust, maar je probeert te passen de pijl, je zal nooit bij zo 'n situatie als volgt.,,, het coördineren van de ruimte, niet een affine coördinatie van De ruimte.En, in feite, de X - en Y - meestal de cartesiaanse coördinaten, zoals blijkt uit onderstaande tabel., en aandacht te schenken aan de horizontale en verticale Maas loodrecht op elkaar.Dit is een affine coördineren de ruimte, maar we kunnen het veranderen als we willen andere affine ruimte.De horizontale en verticale netwerken niet noodzakelijkerwijs verticaal.,,, bijvoorbeeld een affine ruimte, een ruimte affine coördineren, stap 4: een transformatie, zoals je al kan raden, een transformatie zijn vertaling, draaien en reflectie ",,,,, de oorspronkelijke affine affine ruimte, de omvang van de ruimte.,, rekening te houden met de affine ruimte affine ruimte, de helling, draaien en affine ruimte", en, uiteraard, fysische eigenschappen zoals, X, Y, scaleX, zei, draaien, afhankelijk van de ruimte.We bellen als we deze eigenschap, is in feite affine coördinaten, stap 5: het begrip matrix en ik hoop dat het beeld is duidelijk genoeg om de idee van het gezin.Dit is omdat de programmeurs FlashDevelop, zien wij niet in deze netten, Flash ide gemakkelijk een ontwerper.Dit alles moet leven in je hoofd, behalve dat van deze netten, we hebben hulp nodig, matrix.Dus, er is een matrix van de wiskunde is het belangrijk om te begrijpen, dus moeten we de operatie: herziening van de matrix toevoegen en vermenigvuldiging,., stap 6: de matrix toevoegen van beslissende betekenis, de betekenis van de uitdrukking van de geometrie van de matrix.Met andere woorden, je kan je voorstellen hoe zij in een grafiek betekent.Stel dat we in onze ruimte, er waren vier uur, en dan zal ze naar een nieuwe locatie.Dit kan het gebruik van de matrix.Kijk naar de volgende foto 's, zoals je kan zien, hebben we in feite de coördinaten van de vier punten van de ruimte (rood -) naar hier.De uitvoering van deze acties van de symbolen weergegeven:,, zien we ook dat deze verandering in feite worden gebruikt - (ex, ty.Met tussen haakjes en steunen om onderscheid te maken tussen de coördinaten van de vector en statische punten in de ruimte.Ik heb ze in het volgende beeld herschrijven.,, 7: de verwezenlijking van verdere behandelingen, hier is een eenvoudige toevoeging van de verwezenlijking van de matrix.Zie de opmerkingen: het openbaar onderwijs, de uitbreiding van het openbare functies naast Sprite {() {var: de matrix m = nieuwe matrix (); ///////m.tx = stage.stagewidth concretisering matrix * 0,5; ///////dienst m.ty = stage.stageheight * 0,5 X, y d /overdracht: dottedbox = nieuwe dottedbox (); ///////grafische (creëren. De doos is een Sprite) addchild (d); d.transform.matrix = m; ///////toepassing van de matrix van grafische}},, salaristrap 8: de vermenigvuldiging van de geometrie van de matrix te vermenigvuldigen, dan 维尔德贝格尔 matrix toevoegen maar elegant, om de eenvoudige verklaring, maar een beetje ingewikkeld.Zal ik nederig om opnieuw te bevestigen dat het z 'n verklaring.Voor degenen die het begrip voor Linear algebra, waardoor de professor de lezingen, laten we beginnen met de behandeling van de identiteit van de matrix, voor het geval we weten, de vermenigvuldiging van de matrix, een, door de identiteit van de matrix, ik zal altijd tot een metafoor: 6 × 1, in de formule van De geometrische interpretatie, die aanzienlijk vereenvoudiging van de verklaring. Deze uitleg van de formule, cartesiaanse coördinaten (links), 2, 1).Als we nu gaan dit oorspronkelijke rooster en een nieuw netwerk (de juiste maaswijdte), op basis van een reeks vectoren (de volgende rechts -), blauwe zal verschuiven naar de 2 (1) van de nieuwe - - maar als we in de oorspronkelijke net, het is hetzelfde.Omdat we de oorspronkelijke net omgezet in een andere delen van dezelfde vector - zijn wij van mening dat er geen verschil.In feite, voor de verandering verandering is nul.Wat is dit, de identiteit van de matrix, geometrisch oogpunt, maar als we proberen te gebruiken voor de uitvoering van het in kaart brengen van andere omzettingen, zien we wel wat anders.Ik weet dat dit niet een van de meest inspirerende voorbeelden, dus laten we verder gaan met een ander voorbeeld, stap 9 "langs de *, aangegeven: de coördinatie van de ruimte".In het na de verandering van de coördinaten, onderzocht de coördinaten van de vector: na de verandering van de coördinaten van de transformatie van de op twee na de eenheid, de blauwe coördinaten (2 - 1).Maar als je een poging om dit de coördinaten van het veranderen van de mazen in de oorspronkelijke rooster, het is (4, 1), het volledige beeld van gedachten is boven.Deze formule?De resultaten moeten in overeenstemming zijn met het, laten we eens kijken, ik ben er zeker van dat je weet dat deze formule.Nu, ik heb nog hun betekenis, en kijk ons nu. De omvang van de resultaten van de oorspronkelijke coördineren:.,, - (2 - 1), bij de omzetting van de vector: as 2 0), de omschakeling van de y - as vector: (0, 1), de verwachte resultaten: (2 × 2 0 1 0 + * * * * * * * * * * * * * * * * * * * * * 1, 2 + 1) = (4, 1),, ze zijn het niet eens met elkaar.Nu kunnen we blij zijn als de toepassing van het idee van de omschakeling naar de andere.Maar voordat dit een script bereikt.,, 10 stappen: uitvoering van onderzoek dat script, behandelingen (en de daaruit volgende SWF 's).Dat is de doos, een overlapping is langs de * * * * * * * * * * * * * * * * * * * * * II.Ik met nadruk op de belangrijke waarden.Deze waarden moeten worden aangepast, en in de latere stappen van vertegenwoordigers van verschillende transformatie, de diversificatie van de soorten openbare functie Sprite {vermenigvuldiging () {var.: dottedbox = nieuwe dottedbox (); ///////tot verwijzing van grafische addchild (ref.); ref.x = stage.stagewidth × 0,5; ref.y = stage.stageheight × 0,5; var: de matrix m m m m m m = nieuwe matrix (); ///////concretisering matrix m.tx = stage.stagewidth × 0,5; ///////dienst m.ty = stage.stageheight * 0,5 X, y punt = 2 //dienst; de voorbereidende = 0; motor boot stoomboot = 0; md = 1; var D:dottedbox = nieuwe dottedbox (); ///////(d) grafische addchild creëren.; d.transform.matrix = m ///////toepassing van de matrix in onze grafische}}, stap 11:, "X - en Y - hebben Wij de uitbreiding van het elektriciteitsnet.Langs de X - en Y - as van de twee factoren.Blauw is in punt 2 (1), in de oorspronkelijke net vóór de hervorming, en lid 4, 2) de wijziging in de oorspronkelijke net na.- natuurlijk, het is nog steeds in (2, 1), de nieuwe, net na de dienst.) en dat de resultaten van de numerieke... En, en, en...Ze heeft een wedstrijd.In de uitvoering van dit script zien, maar de waarde van veranderingen, doctor in de geneeskunde, van 1 tot 2.,, en ik geloof dat op dit punt, wil je het proberen, dus om zich aan te passen, de y - as van richting veranderd, met behoud van de X - as, twee co - locatie, ik heb twee gevallen de volgende Flits.Lezers die wil helpen deze waarde, kijk, multiplication_final.as, in de source code, stap 14: draaien, draaien, ben ik van mening dat verstoring van de subgroep.Het enige verschil is en, bij toerbeurt, een eenheid van de omvang van de X - en Y - as ongewijzigd blijven, omdat deze twee verticale as tussen de behandelingen verstrekt.,, in feite, matrix, rotate (), en dit te doen.Maar laten we dit toch door te gaan, en we willen niet veranderen in een eenheid van lengte van het net, de omvang van de veranderingen in de richting, maar elke.We kunnen gebruik maken van de resultaten van de driehoek op de hierboven weergegeven.Als gevolg van een roterende, vanuit het oogpunt van de vector, zullen we de gewenste resultaten (omdat, veroordeeld en een X - as), omdat een) y - as.Elke nieuwe van de omvang van de schacht is nog steeds een eenheid, maar elke as een hoek van het origineel in het script, en dat, in de veronderstelling dat, vanuit het oogpunt van 45 graden, is (d.w.z. 0,25 * rad), aanpassing van de waarde var. Het volgende is de matrix, een aantal punten = 0,25 * math.pi = wiskunde. Want a); de voorbereidende = 1 * wiskunde. Misdaad (een); motor boot stoomboot = wiskunde. Misdaad (een); md = wiskunde. Omdat (a); de integriteit van de source code kan worden verwezen, multiplication_final.,,, een stap in de goede richting. 15: toepassing van een 2x2 matrix verklaring voor ons openen. De verkenning van de ruimte.Bij de behandeling van de aanvragen (, linebitmapstyle bitmap linegradientstyle BitmapData,,,,, enz.) is veel maar ik denk dat ik het zou redden van een andere les.In deze zaak, en we zullen proberen te verstoren wij elfen in werking, het ziet er naar uit dat het in feite de flip -.,,, een pseudo - 3D - neutraliteit van de wereld, uit het bovenstaande kan je beelden zien, in een wereld met een identieke standpunten, een grafische station 'op de y - as - voortdurend. De X - as draaien, vector.Aandacht, de X - en Y - as van de eenheid van lengte niet verandert, met andere woorden, geen dimensie moet worden in de as, maar rond de X - as, dit is in de flash van dit idee van een voorbeeld.Klik op het podium overal rond, en begint met een vis zien maken.Stop je vrijlating van interactieve.,, hier een belangrijk punt van de behandelingen.Ik heb er al op gewezen dat de belangrijkste lijnen, de X - as.Je kan ook verwijzen naar de fakeiso.,., de locomotief f1: vis, M - matrix; particuliere var blijkt dat de as X;:, axisy: punt; de functie van fakeiso () {disp = nieuwe punten (stage.stagewidth × 0,5, stage.stageheight × 0,5); m = nieuwe matrix (); m.tx = blijkt X; m.ty = display. Y; ///////verplaatsing naar de fase van de vis (f1) = nieuwe centrum; addchild (f1); f1.transform.matrix = m; ///////de toepassing en omzetting van vis in de as X = nieuwe punten (1 0); ///////axisy vector X - as = nieuwe punten (0, 1); ///////- y - as - fase. AddEventListener (mouseevent.mouse_down, beginnen); ///////addEventListener (mouseevent.mouse_up interactieve fase begonnen. ///////, einde); aan het einde van de particuliere functie begin (E:MouseEvent interactieve} {addEventListener ongeldig): (event.enter f1)._frame, de vernieuwing van de functie aan de (particuliere);} {f1 E:MouseEvent): ongeldig. RemoveEventListener (event.enter_frame, bijgewerkt); particuliere bijwerking van de lijst van kenmerken (e): de gebeurtenissen): {as X ongeldig. (mouseX f1. X, als ratten in de Formule 1. Y); ///////de richting te bepalen mate veranderen (maar oké) as X. Verordening (1); ///////1 eenheid zal apply2matrix () en de nieuwe richting vector omvang; ///////toepassing van de matrix in de private functie apply2matrix (vis) nietig m.setto (as): {x, X, X, y - as. Axisy. X, X, Y, axisy. Y vertonen. Tonen.); f1.transform.matrix = m;}, hier, ik gebruik het opslaan van klasse 16.,, stap: toevoeging van toetsenbord controle, in dit stadium, we zullen proberen toe te voegen aan de controle van het toetsenbord.De positie van de vis die op basis van de snelheid van het tempo van de aanpassing.We zullen de positieve stappen (gedefinieerd als de wijzers van de klok mee draaien en negatieve (tegen de wijzers van de klok mee draaien, en de snelheid van de nieuwe punten. = (1 0); ///////axisy Velo definieert as = nieuwe punten (0, 1); delta_positive = nieuwe matrix (); delta_positive roterende (math.pi × 0,01).; ///////is overgedragen delta_negative = nieuwe matrix (); delta_negative. Roterende (math.pi * 0,01); ///////omkering in de pers een belangrijke, snelheid, draaien, private functie keyup (E: mobiele): invaliditeit ({als = = toetsenbord. Links) (toerental = delta_negative transformpoint (snelheid.) ///////snelheid tegen de wijzers van de klok in} anders als (vrouw = = toetsenbord. Rechts) (toerental = delta_positive. Transformpoint (Velo) ///////rotatiesnelheid van De wijzers van de klok in}}, nu voor elk beeld, we zullen proberen.Vis is positief, met vis.Als de snelheid, snelheid, zijn er meer dan 1, de omvang van de toepassing van het vis, zullen we de matrix, m, krijgen we een goede "effect, en dus om de mogelijkheid uit te sluiten dat het herstel van de normale snelheid zullen we, dan zijn alleen van toepassing op de matrix van vis, De actualisering van particuliere functie. E: gebeurtenissen): ongeldige {VAR front_side: booleaanse = snelheid. X > 0 ///////inspectie van vis (positieve als front_side) {f1). Colorbody (0x002233,0.5)} /kleur vis andere f1 positief. Colorbody (0xffffff, 0,5) /witte Vis disp = geeft aan de achterkant van toepassing. De toevoeging van (Velo); ///////bijwerking de verplaatsing van de huidige en de snelheid van de VAR - velo_norm: punt = snelheid (); ///////0, als de snelheid > we moeten de berekening van 1 eenheid van lengte X velo_norm. Code (1); ///////nDe X - as van OTE zal worden uitgevoerd, meer dan 1 ".We willen niet dat nu m.setto (velo_norm. X, Y, velo_norm. Axisy. X, Y, axisy. X, Y. Weergegeven.); f1.transform.matrix = m;}, stap 17: je vis, klik, en op de linker, pijl om vis te veranderen van richting, 18, stappen.: een Andere toetsenbord controle, specerijen, wat maakt de y - as vector controle. Privé - functie keyup (E: mobiele): invaliditeit ({als = = toetsenbord. Links) (toerental = delta_negative. Transformpoint (Velo)} anders als (kan = = toetsenbord. Rechts) (toerental = delta_positive. Transformpoint (Velo)} als (= = toetsenbord) {axisy = delta_negative. Transformpoint (axisy)} anders als (vrouw = = toetsenbord.) {axisy = delta_positive transformpoint (as.Y)}}, ook de positieve beschikking van vis, nu moeten we de y - as in.De volgende code: var front_side: * * * * * * * axisy booleaanse = X. Y > 0 als (front_side {f1). Colorbody (0x002233,0.5} andere f1). Colorbody (0xffffff, 0,5), stap je niet zo, 19: gewone vis, nou, een controle van de as kan Het resultaat van een beetje in de war. Maar het probleem is dat je nu kan je de vis, het weerspiegelt de vertaling, het eens draaien.Probeer + links. Rechts, Combo, + links. Rechts,.,,, en kijk of je kan blijven "vis -" op de ene zijde (vis grijs).Tip: voortdurend Mining, dan links, en dan naar beneden, en dan naar rechts.Je doet een rotatie.CONCLUSIE, ik hoop dat u bij het lezen van dit na het vinden van een waardevolle aanwinst voor je project.Ik wil schrijven over 2x2 matrix in een tak van de toepassing van artikelen uit de kleine vaardigheden, Matrix3d, dit is een 3D - operatie, van essentieel belang is.Voor de lezing van dank, bedankt.