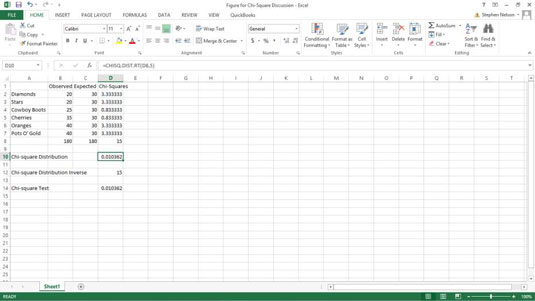
nogle statistiske foranstaltninger i excel - kan være forvirrende, men chi - square funktioner er praktisk.selv hvis du ’ skal kun bruge én af chi - square funktioner, læst alle tre funktion beskrivelser.betragtes som et sæt af statistiske værktøjer, funktioner, få lidt mere følelse.,, chisq.dist.rt: chi - square distribution, chisq.dist.rt funktion, som beregner den ikke skygget sandsynligheden for, at en chi2 distribution, beregner størrelsen af betydning ved hjælp af chi - square værdi og grader af frihed.chi - square værdi er lig med summen af kvadratet standardiserede scorer.den funktion, anvender syntaks = chisq. dist.rt (, x,,, deg_freedom,), hvor x er lig med chi - square værdi, og deg_freedom, svarer til den grad af frihed, som et eksempel på, hvordan det virker, hvis du og’ er mere end en smule mistænksom over for visse ankomst - og afgangstidspunkter en maskine, der viser en af seks billeder: diamanter, stjerner, cowboy - støvler, kirsebær, appelsiner, eller en masse guld.med seks muligheder, man kunne forvente, at i en stor stikprøve, hver af de seks muligheder forekommer ca. en sjettedel af tiden. siger, at stikprøvestørrelsen er 180, f.eks.i dette tilfælde, kunne man forvente, at de enarmede mulighed er 30 gange fordi 180 /6 svarer til 30.hvis du bygger en kladde fragment som denne, du kunne analysere den enarmede bandit., at beregne størrelsen af den betydning og den chi - square fordelingsfunktion, du kunne komme ind i følgende formel til d10: = chisq. dist.rt (d8,5), den funktion, returnerer den værdi 0.010362338, som er niveauet af betydning at en chi - square værdi af 15 skyldes stikprøvefejl, celle d8 er chi - square værdi, som simpelthen er summen af kvadratet forskelle mellem den observerede og forventede værdier.for eksempel, værdien i celle d2 er beregnet ved anvendelse af formlen = + (b2 - – c) <, 2 /c2 til at vende tilbage til den værdi, 3.333333333.det tilsvarende formler i intervallet d3: d7 beregne groft tildannet forskelle for de øvrige spillemaskine symboler.og, forresten, formlen i celle d8 er = summen (d2: d7), sidste linje: det er ’ ser ikke godt ud, vel?der ’ er kun en 1-percent chance for, at den enarmede, at du og’ er bekymret for faktisk kunne producere de observerede værdier på grund af en chance.meget mistænksomt.,, chisq.dist: chi - square distribution, chisq.dist funktion, ligner den chisq.dist.rt funktion, men beregner, venstre skygget, sandsynligheden for, at en chi2 distribution.den funktion, anvender syntaks = chisq. dist (x, deg_freedom, kumulative), hvor x er lig med chi - square værdi, deg_freedom, svarer til den grad af frihed, og de er et skift i sat til 0 eller falsk, hvis du ønsker at beregne sandsynlighed tæthed og 1 eller, hvis man ønsker at beregne en kumulativ sandsynlighed.,, chisq.inv.rt: ikke skygget chi - square distribution sandsynlighed, chisq.inv.rt funktion, returnerer den modsatte af den rigtige skygget sandsynligheden for, at en chi - square distribution.den funktion, anvender syntaks = chisq. inv.rt (sandsynlighed for, deg_freedom), hvor sandsynligheden, er lig med størrelsen af betydning, og deg_freedom, svarer til den grad af frihed,. for at vise et eksempel på chisq.inv.rt funktion, henviser til den arbejdsplan fragment.med seks mulige resultater på den enarmede. du har fem grader af frihed.derfor, hvis du ønsker at beregne chi - square, at ’ s svarende til en 0.010362338 niveau af betydning, kan du træde ind i følgende formel i celle d12: = chisq. inv.rt (d10,5), denne funktion, returnerer den værdi 14.99996888, som er temmelig tæt på 15.bemærk, at d10 anvendes som den første sandsynlighed argument, fordi den celle er niveauet af betydning, som beregnet af chisq.dist funktion.,, chisq.inv: venstre skygget chi - square distribution sandsynlighed, chisq.inv funktion vender tilbage ved hjælp af sandsynligheden for, at en chi - square distribution.den funktion, anvender syntaks = chisq. inv (sandsynlighed for, deg_freedom), hvor sandsynligheden, er lig med størrelsen af betydning, og deg_freedom, svarer til den grad af frihed, til at beregne chi - square værdi at ’ s svarende til en 0.010362338 niveau af betydning med 5 grader af frihed, du kan komme ind følgende formel i en celle i den arbejdsplan: = chisq. inv (0.010362338,5), denne funktion, returnerer den værdi. 562927.,, chisq.test: chi - square test, en chi2 test funktion, kan man vurdere, om forskelle mellem den observerede og forventede værdier repræsenterer chance, eller stikprøvefejl., funktion anvendelser syntaksen, = chisq. test (actual_range, expected_range), henviser til den mistænkelige spillemaskine, kunne du udførelsenrm a chi2 test ved at indtaste følgende formel i celle d14 og at sammenligne, hvad de hører med, hvad du forventer: = chisq. test (b2 - b7 -, c2: c7), den funktion, returnerer den p - værdi eller sandsynlighed, der er vist i celle d14, med angivelse af, at kun en 1.0362-percent chance, at forskellene mellem den observerede og forventede resultater stammer fra stikprøvefejl. er et fælles træk ved en chi2 test er sammenligning af p - værdi og— den værdi, som chisq.test funktion vender tilbage og— til et niveau af betydning.for eksempel, i tilfælde af mistanke, enarmede, kunne man sige, og“, fordi det ’ er ikke muligt at være 100 procent sikker på, vi ’ vil sige, at vi ønsker en 95% sandsynlighed for, hvilket svarer til 5 procents niveau af betydning. ”. hvis p - værdien er mindre end niveauet af betydning, tror du, der er noget galt.statistikere, ikke lyde sådan et fjols, er et udtryk for dette noget er mistænkeligt konklusion:, at afvise nulhypotesen.,,,